Python机器学习入门

第一章 机器学习概述

---

机器学习是从数据中自动分析获得模型，并利用模型对未知数据进行预测

数据集的构成

• 结构：特征值 + 目标值

机器学习算法分类

• 监督学习

  • 目标值是类别 —— 分类问题
  • 目标值是连续型数据 —— 回归问题

• 无监督学习

  • 没有目标值 —— 无监督学习

监督学习(supervised learning)(预测)

• 定义：输入数据是由输入特征值和目标值所组成，函数的输出可以是一个连续的值(称为回归)，或是输出是有限个离散值(称作分类)
• 分类k-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归
• 回归 线性回归、岭回归

无监督学习(unsupervised learning)

• 定义：输入数据是由输入特征值所组成
• 聚类 k-means

开发流程

• 获取数据
• 数据处理
• 特征工程
• 机器学习算法训练 - 模型
• 模型评估
• 应用

---

第二章 特征工程

---

2.1 数据集

---

可用数据集

• 公司内部 百度
• 数据接口 付费
• 数据集：
  • sklearn
  • kaggle
  • UCI

2.1.1 Scikit-learn

• Python语言的机器学习工具
• Scikit-learn包括许多知名的机器学习算法的实现
• Scikit-learn文档完善，有丰富的API
• 1.7.1

sklearn.datasets

• 加载获取流行数据集
• datasets.load_*()
  • 获取小规模数据集，数据包含在datasets里
• datasets.fetch_*(data_home = None)
  • 获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录，默认是～/scikit_learn_data/

sklearn小数据集

• sklearn.datasets.load_iris()

加载并返回鸢尾花数据集

名称	数量
类别	3
特征	4
样本数量	150
每个类别数量	50

• sklearn.datasets.load_boston()

加载并返回波士顿房价数据集

名称	数量
目标类别	5-50
特征	13
样本数量	506

sklearn大数据集

• sklearn.datasets.fetch_20newgroups(data_home = None, subset = ‘train’)
  • subset: ‘train’或者’test’, ‘all’，可选，选择要加载的数据集
  • 训练集的”训练”，测试集的”测试”，两者的”全部”

数据集返回值

• load和fetch返回的数据类型datasets.base.Bunch(字典格式)
  • data：特征数据数组，是[n_samples * n_features]的二维numpy.ndarray数组
  • target：标签数组，是n_samples的一维numpy.ndarray数组
  • DESCR：数据描述
  • feature_names：特征名，新闻数据，手写数字、回归数据集没有
  • target_names：标签名

数据集的划分

机器学习一般的数据集汇划分为两个部分：

• 训练数据：用于训练，构建模型
• 测试数据：在模型检验时使用，用于评估模型是否有效

划分比例：

• 训练集：70% 80% 75%
• 测试集：30% 20% 25%

数据集划分api

• sklearn.model_selection.train_test_split(arrays, *options)
  • x 数据集的特征值
  • y 数据集的标签值
  • test_size测试集的大小，一般为float
  • random_state随机数种子，不同的种子会造成不同的随机采样结果，相同的种子采样结果相同
  • return训练集特征值，测试集特征值，训练集目标值，测试集目标值

---

2.2 特征工程介绍

---

特征工程时使用专业背景知识和技巧处理数据，使得特征能在机器学习算法上发挥更好的作用的过程

• 意义：会直接影响机器学习的效果

特征工程位置与数据处理的比较

• pandas：一个数据读取非常方便以及基本的处理格式的工具
• sklearn：对于特征的处理提供了强大的接口

特征工程包含内容

• 特征抽取
• 特征预处理
• 特征降维

---

2.3 特征抽取

---

将任意数据(如文本或图像)转换为可用于机器学习的数字特征

• 字典特征提取(特征离散化)
• 文本特征提取
• 图像特征提取(深度学习介绍)

特征提取API

• sklearn.feature_extraction

2.3.1 字典特征提取

作用：对字典数据进行特征值化

• sklearn.feature_extraction.DictVectorizer(sparse = Ture,…)
  • DictVectorizer.fit_transform(X) X：字典或者包含字典的迭代器 返回值：返回sparse(稀疏)矩阵
  • DictVectorizer.inverse_transform(X) X：array数组或者sparse矩阵 返回值：转换之前数据格式
  • DictVectorizer.get_feature_names_out() 返回类别名称

稀疏矩阵：将非0值 按位置表示出来

import sklearn
from sklearn.feature_extraction import DictVectorizer

data = [{'city': '北京', 'temperature': 100},
      {'city': '上海', 'temperature': 60},
      {'city': '深圳', 'temperature': 30}]

# 实例化类DictVectorizer
transfer = DictVectorizer()
# 调用fit_transform方法输入数据并转换
data_new = transfer.fit_transform(data)

print(data_new) # 没有加上sparse = False参数的结果
# <Compressed Sparse Row sparse matrix of dtype 'float64'
# 	with 6 stored elements and shape (3, 4)>
#   Coords	Values
#   (0, 1)	1.0
#   (0, 3)	100.0
#   (1, 0)	1.0
#   (1, 3)	60.0
#   (2, 2)	1.0
#   (2, 3)	30.0

transfer = DictVectorizer(sparse = False)
print(data_new)
# [[  0.   1.   0. 100.]
#  [  1.   0.   0.  60.]
#  [  0.   0.   1.  30.]]

print(transfer.get_feature_names_out())
# ['city=上海' 'city=北京' 'city=深圳' 'temperature']

对于特征当中存在的类别信息，都会做one-hot编码处理

2.3.2 文本特征提取

作用：对文本数据进行特征值化

• sklearn.feature_extraction.text.CountVectorizer(stop_words = []) stop_words 停用词
  • 返回词频矩阵
• CountVectorizer.fit_transform(X) X：文本或者包含文本字符串的可迭代对象 返回值：返回sparse矩阵
• CountVectorizer.inverse_transform(X) X：array数组或者sparse矩阵 返回值：转换之前数据格式
• CountVectorizer.get_feature_names_out() 返回值：单词列表
• sklearn.feature_extranction.text.TfidfVectorizer

from sklearn.feature_extraction.text import CountVectorizer

data = ["life is short, i like python",
        "life is too long, i dislike python"]

transfer = CountVectorizer()
data_new = transfer.fit_transform(data)

print(data_new.toarray()) # 统计每个样本特征词出现的个数
print(transfer.get_feature_names_out())

# [[0 1 1 1 0 1 1 0]
#  [1 1 1 0 1 1 0 1]]
# ['dislike' 'is' 'life' 'like' 'long' 'python' 'short' 'too']

中文分词，jieba

jieba.cut()

• 返回词语组成的生成器

from idlelib.pyparse import trans

import jieba
from sklearn.feature_extraction.text import CountVectorizer

data = ["活着的意义，不是为了死去，而是为了活着本身。",
        "活着本身就有一种力量，这种力量支撑着我们度过苦难，也让我们在苦难中依然能够感受到生活的温暖。"]

data_new = []
for text in data:
    data_new.append(" ".join(list(jieba.cut(text))))

transformer = CountVectorizer()
X_transformed = transformer.fit_transform(data_new)
print(X_transformed.toarray())
print(transformer.get_feature_names_out())

# [[0 1 2 0 0 0 1 0 0 0 1 1 2 0 0 1 0 0 0]
#  [1 0 0 1 2 1 0 1 2 1 1 0 1 1 1 0 1 2 1]]
# ['一种' '不是' '为了' '依然' '力量' '度过' '意义' '感受' '我们' '支撑' '本身' '死去' '活着' '温暖'
#  '生活' '而是' '能够' '苦难' '这种']

2.3.3 Tf-idf文本特征提取

• TF-IDF的主要思想是：如果某个词或短语在一篇文章中出现的概率高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。
• TF-IDF作用：用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度

公式

• 词频(term frequency，tf)指的是某一个给定的词语在该文件中出现的频率
• 逆向文档频率(inverse document frequency，idf)是一个词语普遍重要性的度量，某一特定词语的idf，可以由总文件数目除以包含该词语之文件的数目，再将得到的商取以10为底的对数得到

API

• sklearn.feature_extraction.text.TfidfVectorizer(stop_words = None,…)

• 返回词的权重矩阵

  • TfidfVectorizer.fit_transform(X)

    • X：文本或者包含文本字符串的可迭代对象

    • 返回值：返回sparse矩阵

  • TfidfVectorizer.inverse_transform(X)

    • X：array数组或者sparse矩阵
    • 返回值：转换之前数据格式

  • TfidfVectorizer.get_feature_names_out()

    • 返回值：单词列表

from idlelib.pyparse import trans

import jieba
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer

data = ["活着的意义，不是为了死去，而是为了活着本身。",
        "活着本身就有一种力量，这种力量支撑着我们度过苦难，也让我们在苦难中依然能够感受到生活的温暖。"]

data_new = []
for text in data:
    data_new.append(" ".join(list(jieba.cut(text))))

transformer = TfidfVectorizer()
X_transformed = transformer.fit_transform(data_new)
print(X_transformed.toarray())
print(transformer.get_feature_names_out())

# Building prefix dict from the default dictionary ...
# Loading model from cache /var/folders/vv/y2k4cvj91fjbmw1cp4415wtr0000gn/T/jieba.cache
# [[0.         0.30814893 0.61629785 0.         0.         0.
#   0.30814893 0.         0.         0.         0.2192505  0.30814893
#   0.438501   0.         0.         0.30814893 0.         0.
#   0.        ]
#  [0.21314023 0.         0.         0.21314023 0.42628046 0.21314023
#   0.         0.21314023 0.42628046 0.21314023 0.15165103 0.
#   0.15165103 0.21314023 0.21314023 0.         0.21314023 0.42628046
#   0.21314023]]
# ['一种' '不是' '为了' '依然' '力量' '度过' '意义' '感受' '我们' '支撑' '本身' '死去' '活着' '温暖'
#  '生活' '而是' '能够' '苦难' '这种']
# Loading model cost 0.264 seconds.
# Prefix dict has been built successfully.

---

2.4 特征预处理

---

通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程

数值型数据的无量纲化

• 归一化
• 标准化

特征预处理API

• sklearn.preprocessing

特征的单位或者大小相差较大、或者某些特征的方差相比其他的特征要大出几个数量级，容易影响(支配)目标结果，使得一些算法无法学习到其它的特征

2.4.1 归一化

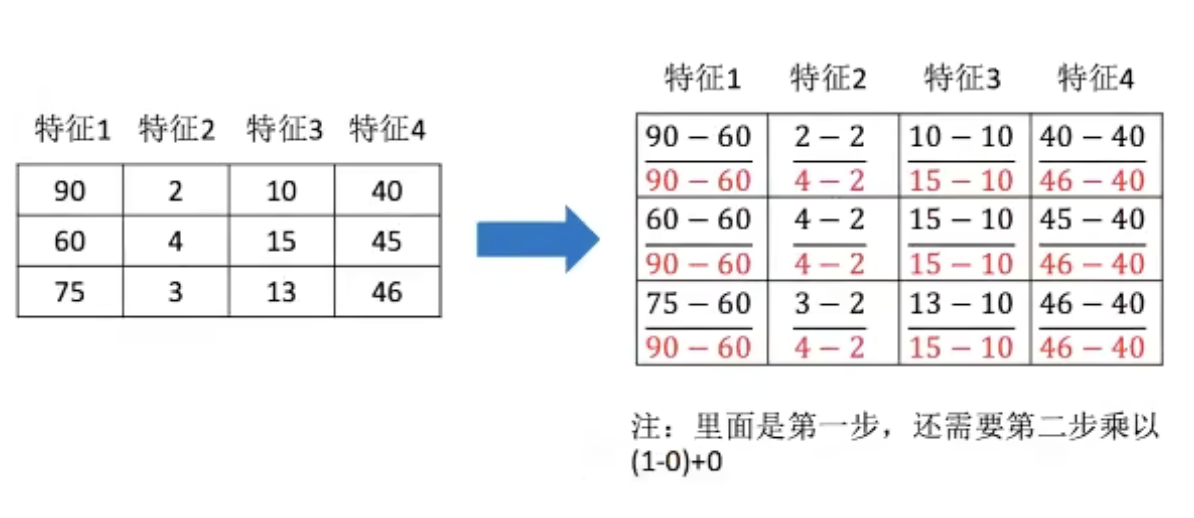
通过对原始数据进行变换把数据映射到(默认为[0, 1])之间

公式
$$
X’ = \frac{x - min}{\max-min}
$$

$$
X’’ = X’ * (mx - mi) + mi
$$

作用于每一列，max为一列的最大值，min为一列的最小值，那么X’’为最终结果，mx、mi分别为指定区间值，默认mx为1，mi为0

API

• sklearn.preprocessing.MinMaxScaler(feature_range = (0, 1)…)
  • MinMaxScalar.fit_transform(X)
    • X：numpy array格式的数据[n_samples, n_features]
  • 返回值：转换后的形状相同的array

transfer = MinMaxScaler()
data_new = transfer.fit_transform(data)

缺点：最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性(稳定性)较差，只适合传统精确小数据场景

2.4.2 标准化

通过对原始数据进行变换把数据变换到均值为0，标准差为1范围内
$$
X’ = \frac{x - mean}{σ}
$$
作用于每一列，mean为平均值，σ为标准差

• 对于归一化来说：如果出现异常点，影响了最大值和最小值，那么结果显然会发生改变
• 对于标准化来说：如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大，从而方差改变较小

API

• sklearn.preprocessing.StandardScaler()
  • 处理之后，对每列来说，所有数据都聚集在均值为0附近，标准差为1
  • StandardScaler.fit_transform(X)
    • X：numpy array格式的数据[n_samples, n_features]
  • 返回值：转换后的形状相同的array

在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景

---

2.5 特征降维

---

降维是指在某些限定条件下，降低随机变量(特征)个数，得到一组”不相关”主变量的过程

• 降低随机变量的个数
• 相关特征(correlated feature)
  • 相对湿度与降雨量之间的相关
  • 等的

正是因为在进行训练的时候，我们都是使用特征进行学习，如果特征本身存在问题或者特征之间相关性较强，对于算法学习预测会影响较大

两种降维方式

• 特征选择
• 主成分分析(一种特征提取的方式)

2.5.1 特征选择

数据中包含冗余或相关变量(或称特征、属性、指标等)，旨在从原有特征中找出主要特征

方法

• Filter(过滤式)：主要探究特征本身特点、特征与特征和目标值之间关联
  • 方差选择法：低方差特征过滤
  • 相关系数
• Embedded(嵌入式)：算法自动选择特征(特征与目标值之间的关联)
  • 决策树：信息熵、信息增益
  • 正则化：L1、L2
  • 深度学习：卷积等

模块

• sklearn.feature_selection

过滤式

一、低方差特征过滤

删除低方差的一些特征

• 特征方差小：某个特征大多样本的值比较相近
• 特征方差大：某个特征很多样本的值都有差别

API

• sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
  • 删除所有低方差特征
  • Variance.fit_transform(X)
    • X：numpy array格式的数据[n_samples, n_features]
    • 返回值：训练集差异低于threshold的特征将被删除，默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征

transfer = VarianceThreshold()
data_new = transfer.fit_transform(data)

二、相关系数
$$
r=\frac{n \sum x y-\sum x \sum y}{\sqrt{n \sum x^{2}-\left(\sum x\right)^{2}} \sqrt{n \sum y^{2}-\left(\sum y\right)^{2}}}
$$
特点

相关系数的值介于-1与+1之间，即-1 <= r <= 1，其性质如下：

• 当 r > 1时，表示两变量正相关，r < 0时，两变量为负相关
• 当 |r| = 1时，表示两变量为完全相关，当r = 0时，表示两变量间无相关关系
• 当 0 < |r| < 1 时，表示两变量存在一定程度的相关。且|r|越接近1，两变量间线性关系越密切；|r|越接近于0，表示两变量的线性相关越弱
• 一般可按三级划分：|r| < 0.4为低度相关；0.4 <= |r| < 0.7为显著性相关；0.7 <= |r| < 1为高度线性相关

API

• from scipy.stats import pearsonr
  • x：(N,) array_like
  • y：(N,) array_like Returns：(Pearson’s correlation coeffcient，p-value)

---

2.6 主成分分析(PCA)

---

高维度数据转化为低纬度数据的过程，在此过程中可能会舍弃原有数据、创造新的变量

作用：时数据维数压缩，尽可能降低原数据的维数(复杂度)，损失少量信息

应用：回归分析或者聚类分析当中

API

• sklearn.decomposition.PCA(n_components = None)
  • 将数据分解为较低维数空间
  • n_components：
    • 小数：表示保留百分之多少的信息
    • 整数：减少到多少特征
  • PCA.fit_transform(X) X：numpy array格式的数据 [n_samples, n_features]
  • 返回值：转换后指定维度的array

---

第三章 分类算法

---

3.1 sklearn转换器和估计器

---

转换器——特征工程的父类

特征工程的接口称之为转换器，其中转换器调用有这么几种形式

• fit_transform
• fit
• transform

1、实例化(实例化的是一个转换器类(Transformer))

2、调用fit_transform(对于文档建立分类词频矩阵，不能同时调用)

标准化：

(x - mean) / std

fit_transform()

• fit() 计算 每一列的平均值、标准差
• transform() (x - mean) / std进行最终的转换

估计器——sklearn机器学习算法的实现

在sklearn中，估计器(estimator)是一个重要的角色，是一类实现了算法的API

1、用于分类的估计器：

• sklearn.neighbors k-近邻算法
• sklearn.naive_bayes 贝叶斯
• sklearn.linear_model.LogisticRegression 逻辑回归
• sklearn.tree 决策树与随机森林

2、用于回归的估计器

• sklearn.linear_model.LinearRegression 线性回归
• sklearn.linear_model.Ridge 岭回归

3、用于无监督学习的估计器

• sklearn.cluster.KMeans 聚类

1、实例化一个estimator

2、estimator.fit(x_train, y_train)计算——调用完毕，模型生成

3、模型评估

• 直接比对真实值和预测值
  • y_predict = estimator.predict(x_test)
  • y_test == y_predict
• 计算准确率
  • accuracy = estimator.score(x_test, y_test)

---

3.2 K-近邻算法

---

如果一个样本在特征空间中的k个最相似(即特征空间中最临近)的样本中的大多数属于某一个类别，则该样本也属于这个类别

来源：KNN算法最早是由Cover和Hart提出的一种分类算法

距离公式

两个样本的距离可以通过如下公式计算，又称欧式距离
$$
比如说，a(a1, a2, a3), b(b1, b2, b3)\ \sqrt{(a 1-b 1)^{2}+(a 2-b 2)^{2}+(a 3-b 3)^{2}}
$$

API

• sklearn.neighborsClassifier(n_neighbors = 5, algorithm = ‘auto’)
  • n_neighbors：int 可选(默认 = 5) k_neighbors查询默认使用的邻居数
  • algorithm：{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}，可选用于计算最近邻居的算法(不同实现方式影响效率)
    • ‘ball_tree’将会使用BallTree
    • ‘kd_tree’将使用KDTree
    • ‘auto’将尝试根据传递给fit方法的值来决定最合适的算法

案例 预测鸢尾花

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler


def knn_iris():
    """
    使用KNN 算法对鸢尾花进行分类
    :return:
    """
    # 1、获取数据
    iris = load_iris()

    # 2、划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state = 6)

    # 3、特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4、KNN算法预估器
    estimator = KNeighborsClassifier(n_neighbors = 3)
    estimator.fit(x_train, y_train)

    # 5、模型评估
    y_predict = estimator.predict(x_test)
    print("y_predict:" , y_predict)
    print("对比真实值和预测值：", y_test == y_predict)

    score = estimator.score(x_test, y_test)
    print("准确率：", score)
    return None

if __name__ == "__main__":
    knn_iris()
    
# y_predict: [0 2 0 0 2 1 1 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1 2]
# 对比真实值和预测值： [ True  True  True  True  True  True False  True  True  True  True  True
#   True  True  True False  True  True  True  True  True  True  True  True
#   True  True  True  True  True  True  True  True  True  True False  True
#   True  True]
# 准确率： 0.9210526315789473

优点

• 简单，易于理解，易于实现，无需训练

缺点

• 懒惰算法，对测试样本分类时的计算量大，内存开销大
• 必须指定k值，k值选择不当则分类精度不能保证

使用场景

• 小数据场景，几千～几万样本，具体场景具体业务去测试

---

3.3 模型选择与调优

---

3.3.1 交叉验证

交叉验证：将拿到的训练数据，分为训练和验证集，如 将数据分成4份，其中一份作为验证集，然后经过4次(组)的测试，每次都更换不同的验证集，即得到4组模型的结果，取平均值作为最终结果，又称4折交叉验证

3.3.2 超参数搜索——网格搜索(Grid Search)

通常情况下，有很多参数是需要手动指定的(如k-近邻算法中的k值)，这种叫超参数，但是手动过程繁杂，所以需要对模型预设几种超参数组合，每组超参数都采用交叉验证来进行评估，最后选出最优参数组合建立模型

模型选择与调优API

• sklearn.model_selection.GridSearchCV(estimator, param_grid = None, cv = None)
  • 对估计器的指定参数值进行详尽搜索
  • estimator：估计器对象
  • param_grid：估计器参数(dict){“n_neighbors”: [1, 3, 5]}
  • cv：指定几折交叉验证
  • fit()：输入训练数据
  • score()：准确率
  • 结果分析：
    • 最佳参数：best_params_
    • 最佳结果：best_score_
    • 最佳估计器：best_estimator_
    • 交叉验证结果：cv_results_

鸢尾花

def knn_iris_gscv():
    """
    使用KNN 算法对鸢尾花进行分类, 添加网格搜索和交叉验证
    :return:
    """
    # 1、获取数据
    iris = load_iris()

    # 2、划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state = 6)

    # 3、特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4、KNN算法预估器
    estimator = KNeighborsClassifier(n_neighbors = 3)
    estimator.fit(x_train, y_train)

    # 加入网格搜索和交叉验证
    estimator = GridSearchCV(estimator, param_grid = {'n_neighbors': [1, 3, 5, 7, 9, 11]}, cv = 10)
    estimator.fit(x_train, y_train)

    # 5、模型评估
    y_predict = estimator.predict(x_test)
    print("y_predict:" , y_predict)
    print("对比真实值和预测值：", y_test == y_predict)

    score = estimator.score(x_test, y_test)
    print("准确率：", score)

    print("最佳参数", estimator.best_params_)
    print("最佳结果", estimator.best_score_)
    print("最佳估计器", estimator.best_estimator_)
    print("交叉验证结果", estimator.cv_results_)
    return None
  
# y_predict: [0 2 0 0 2 1 2 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1
#  2]
# 对比真实值和预测值： [ True  True  True  True  True  True  True  True  True  True  True  True
#   True  True  True False  True  True  True  True  True  True  True  True
#   True  True  True  True  True  True  True  True  True  True False  True
#   True  True]
# 准确率： 0.9473684210526315
# 最佳参数 {'n_neighbors': 11}
# 最佳结果 0.9734848484848484
# 最佳估计器 KNeighborsClassifier(n_neighbors=11)
# 交叉验证结果 {'mean_fit_time': array([0.00012665, 0.0001209 , 0.00011959, 0.00011954, 0.00012078,
#        0.0001174 ]), 'std_fit_time': array([1.49413711e-05, 1.09113690e-05, 5.32714825e-06, 4.85601935e-06,
#        5.19424300e-06, 2.41309756e-06]), 'mean_score_time': array([0.00033486, 0.00030804, 0.00029821, 0.00030265, 0.00033834,
#        0.00031242]), 'std_score_time': array([8.85420127e-05, 3.18315144e-05, 1.89715283e-05, 7.72137627e-06,
#        1.12072276e-04, 7.35798518e-06]), 'param_n_neighbors': masked_array(data=[1, 3, 5, 7, 9, 11],
#              mask=[False, False, False, False, False, False],
#        fill_value=999999), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}, {'n_neighbors': 11}], 'split0_test_score': array([1., 1., 1., 1., 1., 1.]), 'split1_test_score': array([0.91666667, 0.91666667, 1.        , 0.91666667, 0.91666667,
#        0.91666667]), 'split2_test_score': array([1., 1., 1., 1., 1., 1.]), 'split3_test_score': array([1.        , 1.        , 1.        , 1.        , 0.90909091,
#        1.        ]), 'split4_test_score': array([1., 1., 1., 1., 1., 1.]), 'split5_test_score': array([0.90909091, 0.90909091, 1.        , 1.        , 1.        ,
#        1.        ]), 'split6_test_score': array([1., 1., 1., 1., 1., 1.]), 'split7_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 1.        ,
#        1.        ]), 'split8_test_score': array([1., 1., 1., 1., 1., 1.]), 'split9_test_score': array([0.90909091, 0.81818182, 0.81818182, 0.81818182, 0.81818182,
#        0.81818182]), 'mean_test_score': array([0.96439394, 0.95530303, 0.97272727, 0.96439394, 0.96439394,
#        0.97348485]), 'std_test_score': array([0.04365767, 0.0604591 , 0.05821022, 0.05965639, 0.05965639,
#        0.05742104]), 'rank_test_score': array([5, 6, 2, 3, 3, 1], dtype=int32)}

---

3.4 朴素贝叶斯算法

---

3.4.1 概率基础

• 概率定义为一件事情发生的可能性

扔出一个硬币，结果头像朝上

P(X)：取值在[0, 1]

朴素：特征与特征之间是相互独立的

3.4.2 联合概率、条件概率与相互独立

• 联合概率：包含多个条件、且所有条件同时成立的概率
  • 记作：P(A, B)
• 条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率
  • 记作：P(A | B)
• 相互独立：如果P(A, B) = P(A)P(B)，则称事件A与事件B相互独立

3.4.3 贝叶斯公式

$$
P(C|W) = \frac{P(W|C)P(C)}{P(W)}
$$

W为给定文档的特征值(频数统计，预测文档提供)，c为文档类别

应用场景：文本分类 (单词作为特征)

那么这个公式如果应用在分章分类的场景中，我们可以这样看：
$$
P(C|F1,F2,…) = \frac{P(F1,F2,…|C)P(C)}{P(F1,F2,…)}
$$
其中c可以是不同类别

公式分为三个部分：

• P(C)：每个文档类别的概率(某文档类别数/总文档数量)
• P(W|C)：给定类型下特征(被预测文档中出现的词)的概率
  • 计算方法：P(F1 | C) = Ni/N(训练文档中去计算)
    • Ni为该F1词在C类别所有文档中出现的次数
    • N为所属类别C下的文档所有词出现的次数和
• P(F1,F2,…)预测文档中每个词的概率

3.4.4 拉普拉斯平滑系数

目的：防止计算出的分类概率为0
$$
P(F1|C) = \frac{Ni + α}{N + αm}
$$

3.4.5 API

• sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
  • 朴素贝叶斯分类
  • alpha：拉普拉斯平滑系数

def nb_news():
    '''
    用朴素贝叶斯算法对新闻进行分类
    :return: 
    '''
    # 1、获取数据
    news = fetch_20newsgroups(subset = 'all')
    
    # 2、划分数据集
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target)
    
    # 3、特征工程：文本特征抽取-tfidf
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    
    # 4、朴素贝叶斯算法预估器流程
    estimator = MultinomialNB()
    estimator.fit(x_train, y_train)
    
    # 5、模型评估
    # 方法一：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:" , y_predict)
    print("直接比对真实值和预测值：", y_test == y_predict)
    
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：", score)
    
    return None
  
# y_predict: [ 4  9  4 ... 16  9 12]
# 直接比对真实值和预测值： [ True  True  True ...  True  True  True]
# 准确率为： 0.8406196943972836

优点：

• 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率
• 对缺失数据不太敏感，算法也比较简单，常用于文本分类
• 分类准确度高，速度快

缺点：

• 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好

---

3.5 决策树

---

一、原理

• 信息熵、信息增益等

二、信息熵的定义

• H的专业术语称之为信息熵，单位为比特

$$
H(X)=-\sum_{i=1}^{n}P\left(x_{i}\right)\log_{b}P\left(x_{i}\right)
$$

三、决策树划分依据之一 信息增益

特征A对训练数据集D的信息增益g(D, A)定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差，即公式为：
$$
g(D,A) = H(D) - H(D|A)
$$

信息熵计算
$$
H(D)=-\sum_{k=1}^{k}\frac{|C_{k}|}{|D|}log\frac{|C_{k}|}{|D|}
$$
条件熵的计算
$$
H(D|A)=\sum_{i=1}^{n}\frac{|D_{i}|}{|D|}H(D_{i}) = -\sum_{i=1}^{n}\frac{|D_{i}|}{|D|}\sum_{k=1}^{k}\frac{|D_{ik}|}{|Di|}log\frac{|D_{ik}|}{|Di|}
$$
Ck表示属于某个类别的样本数

tips：信息增益表示得知特征X的信息而息的不确定性减少的程度使得类Y的信息熵减少的程度

• ID3
  • 信息增益 最大的准则
• C4.5
  • 信息增益比 最大的准则
• CART
  • 分类树：基尼系数 最小的准则 在sklearn中可以选择划分的默认原则
  • 优势：划分更加细腻

3.5.1 决策树API

• class sklearn.tree.DecisionTreeClassifier(criterion = ‘gini’, max_depth = None, random_state = None)
  • 决策树分类器
  • criterion：默认时’gini’系数，也可以选择信息增益的熵’entropy’
  • max_depth：树的深度大小
  • random_state：随机数种子

def decision_iris():
    '''
    用决策树对鸢尾花进行分类
    :return:
    '''
    # 1、获取数据集
    iris = load_iris()

    # 2、划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state = 6)

    # 3、决策树预估器
    estimator = DecisionTreeClassifier(criterion = "entropy")
    estimator.fit(x_train, y_train)

    # 4、模型评估
    # 方法一：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:", y_predict)
    print("直接比对真实值和预测值：", y_test == y_predict)

    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：", score)
    return None
  
# y_predict: [0 2 0 0 2 1 2 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1 2]
# 直接比对真实值和预测值： [ True  True  True  True  True  True  True  True  True  True  True  True
#   True  True  True False  True  True  True  True  True  True  True  True
#   True  True  True  True  True  True  True  True  True  True False  True
#   True  True]
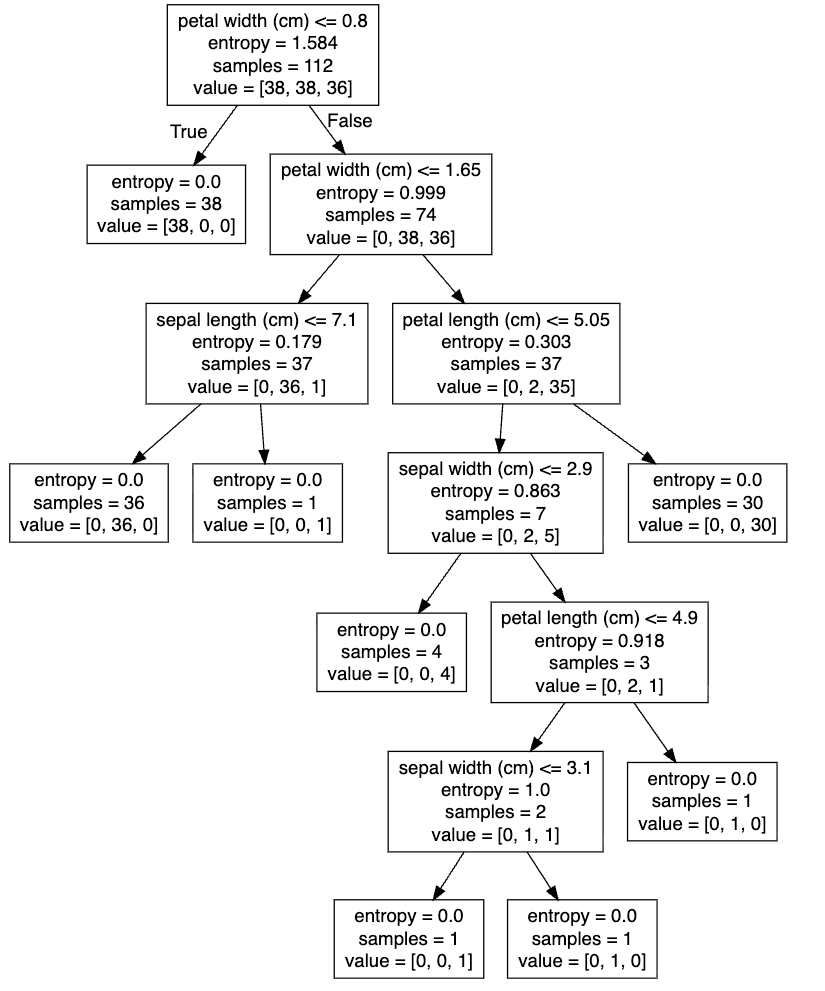
# 准确率为： 0.9473684210526315

3.5.2 决策树可视化

1、保存树的结构到dot文件

• sklearn.tree.export_graphviz()该函数能够导出DOT格式
  • tree.export_graphviz(estimator, out_file = ‘tree.dot’, feature_names = [‘’, ‘’])

优点：

• 简单的理解和解释，树木可视化

缺点：

• 决策树学习器可能会生成过于复杂的树，这些树对训练数据拟合得很好，但对新数据的推广能力很差，这种现象称为过拟合

改进：

• 减枝cart算法(决策树API当中已经实现、随机森林参数调优游相关介绍)
• 随机森林

---

3.6 集成学习方法之随机森林

---

3.6.1 集成学习方法

集成学习通过建立几个模型组合来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和做出预测。这些预测最后结合成组合预测，因此优于任何一个单分类做出的预测

3.6.2 随机森林

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定

3.6.3 随机森林原理过程

学习算法根据下列算法而建造每棵树：

• 用N来表示训练用例(样本)的个数，M表示特征数目
  • 1 一次随机选出一个样本，重复N次，(有可能出现重复的样本)
  • 2 随机去选出m个特征，m << M，建立决策树
• 采取bootstrap抽样

3.6.4 API

• class sklearn.ensemble.RandomForestClassifier(n_estimators = 10, criterion = ‘gini’, max_depth = None, bootstrap = True, random_state = None, min_samples_split = 2)
  • 随机森林分类器
  • n_estimators：integer，optional(default = 10) 森林里的树木数量
  • criterion：string 可选(default = ‘gini’) 分割特征的测量方法
  • max_depth：integer或None，可选(默认 = 无) 树的最大深度 5，8，15，25，30
  • max_features = “auto”，每个决策树的最大特征数量
    • if “auto”, then max_features = sqrt(n_features).
    • if “sqrt”, then max_features = sqrt(n_features). (same as “auto”)
    • if “log2”, then max_features = log2(n_features).
    • if None, then max_features = n_features.
  • bootstrap：boolean，optional(default = True) 是否在构建树时使用放回抽样
  • min_samples_split：节点划分最少样本数
  • min_samples_leaf：叶子节点的最少样本数
• 超参数：n_estimators、max_depth、min_samples_split、min_samples_leaf

---

第四章 回归与聚类算法

---

4.1 线性回归

---

应用场景

• 房价预测
• 销售额度预测
• 金融：贷款额度预测、利用线性回归以及系数分析因子

4.1.1什么是线性回归

线性回归是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式

• 特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归

公式：h(w) = w₁x₁ + w₂x₂ + w₃x₃ + b = w^Tx + b

其中w，x可以理解为矩阵：
$$
\mathrm{w}=\left(\begin{array}{c}b \ w_{1} \ w_{2}\end{array}\right), \mathrm{x}=\left(\begin{array}{c}1 \ x_{1} \ x_{2}\end{array}\right)
$$

线性回归当中线性模型有两种，一种是线性关系，另一种是非线性关系

4.1.2 线性回归的损失和优化原理

1、损失函数

总损失定义为：
$$
J(\theta) = (h_w(x_1) - y_1)^2 + (h_w(x_2) - y_2)^2 + \cdots + (h_w(x_m) - y_m)^2
= \sum_{i=1}^{m} \left( h_w(x_i) - y_i \right)^2
$$

• y_i为第i个训练样本的真实值
• h(x_i)为第i个训练样本特征值组合预测函数
• 又称最小二乘法

2、优化算法

如何去求模型当中的w，使得损失最小(目的是找到最小损失对应的w值)

线性回归经常使用的两种优化算法

• 正规方程

​ w = (X^TX)^-1X^Ty

理解：X为特征值矩阵，y为目标值矩阵，直接求到最好的结果

缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

• 梯度下降

$$
\begin{array}{l}w_{1}:=w_{1}-\alpha \frac{\partial \operatorname{cost}\left(w_{0}+w_{1} x_{1}\right)}{\partial w 1} \ w_{0}:=w_{0}-\alpha \frac{\partial \operatorname{cost}\left(w_{0}+w_{1} x_{1}\right)}{\partial w 1}\end{array}
$$

理解：α为学习速率，需要手动指定(超参数)，α旁边的整体表示方向，沿着这个函数下降的方向找，最后就能找到山谷的最低点，然后更新W值

使用：面对训练数据规模十分庞大的任务，能够找到较好的结果

4.1.3 线性回归API

• sklearn.linear_model.LinearRegression(fit_intercept = True)
  • 通过正规方程优化
  • fit_intercept：是否计算偏置
  • LinearRegression.coef_：回归系数
  • LinearRegression.intercept_：偏置
• sklearn.linear_model.SGDRegressor(loss = “squared_less”, fit_intercept = True, learning_rate = ‘invscaling’, eta0 = 0.01)
  • SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型
  • loss：损失类型
    • loss = “squared_loss”：普通最小二乘法
  • fit_intercept：是否计算偏置
  • learning_rate：string，optional
    • 学习率填充
    • ‘constant’：eta = eta0
    • ‘optimal’：eta = 1.0 / (alpha * (t + t0))[default]
    • ‘invscaling’：eta = eta0 / pow(t, power_t)
      • power_t = 0.25：存在父类当中
    • 对于一个常数值的学习率来说，可以使用learning_rate = ‘constant’，并使用eta0来指定学习率
  • SGDRegressor.coef_：回归系数
  • SGDRegressor.intercept_：偏置

sklearn提供给我们两种实现的API，可以根据选择使用

from sklearn.datasets import fetch_openml
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor

import ssl
import certifi
from sklearn.model_selection import train_test_split

ssl._create_default_https_context = lambda: ssl.create_default_context(cafile=certifi.where())

def linear1():
    '''
    正规方程的优化方法对波士顿房价进行预测
    :return:
    '''
    # 1）获取数据
    boston = fetch_openml(name = 'boston', version = 1, as_frame = True)

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state = 22)

    # 3）标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）预估器
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)

    # 5）得出模型
    print("正规方程-权重系数为: \n", estimator.coef_)
    print("正规方程-偏置为: \n", estimator.intercept_)

    # 6）模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价: \n", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("正规方程-均方误差为: \n", error)

def linear2():
    '''
    梯度下降的优化方法对波士顿房价进行预测
    :return:
    '''
    # 1）获取数据
    boston = fetch_openml(name = 'boston', version = 1, as_frame = True)

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state = 22)

    # 3）标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）预估器
    estimator = SGDRegressor()
    estimator.fit(x_train, y_train)

    # 5）得出模型
    print("梯度下降-权重系数为: \n", estimator.coef_)
    print("梯度下降-偏置为: \n", estimator.intercept_)

    # 6）模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价: \n", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("梯度下降-均方误差为: \n", error)

if __name__ == "__main__":
    # 代码1：正规方程的优化方法对波士顿房价进行预测
    linear1()
    # 代码2：梯度下降的优化方法对波士顿房价进行预测
    linear2()

#正规方程 - 权重系数为:
# [-0.64817766  1.14673408 - 0.05949444  0.74216553 - 1.95515269  2.70902585
#  - 0.07737374 - 3.29889391  2.50267196 - 1.85679269 - 1.75044624  0.87341624
#  - 3.91336869]
# 正规方程 - 偏置为:
# 22.621372031662272
# 预测房价:
# [28.22944896 31.5122308  21.11612841 32.6663189  20.0023467  19.07315705
#  21.09772798 19.61400153 19.61907059 32.87611987 20.97911561 27.52898011
#  15.54701758 19.78630176 36.88641203 18.81202132  9.35912225 18.49452615
#  30.66499315 24.30184448 19.08220837 34.11391208 29.81386585 17.51775647
#  34.91026707 26.54967053 34.71035391 27.4268996  19.09095832 14.92742976
#  30.86877936 15.88271775 37.17548808  7.72101675 16.24074861 17.19211608
#  7.42140081 20.0098852  40.58481466 28.93190595 25.25404307 17.74970308
#  38.76446932  6.87996052 21.80450956 25.29110265 20.427491   20.4698034
#  17.25330064 26.12442519  8.48268143 27.50871869 30.58284841 16.56039764
#  9.38919181 35.54434377 32.29801978 21.81298945 17.60263689 22.0804256
#  23.49262401 24.10617033 20.1346492  38.5268066  24.58319594 19.78072415
#  13.93429891  6.75507808 42.03759064 21.9215625  16.91352899 22.58327744
#  40.76440704 21.3998946  36.89912238 27.19273661 20.97945544 20.37925063
#  25.3536439  22.18729123 31.13342301 20.39451125 23.99224334 31.54729547
#  26.74581308 20.90199941 29.08225233 21.98331503 26.29101202 20.17329401
#  25.49225305 24.09171045 19.90739221 16.35154974 15.25184758 18.40766132
#  24.83797801 16.61703662 20.89470344 26.70854061 20.7591883  17.88403312
#  24.28656105 23.37651493 21.64202047 36.81476219 15.86570054 21.42338732
#  32.81366203 33.74086414 20.61688336 26.88191023 22.65739323 17.35731771
#  21.67699248 21.65034728 27.66728556 25.04691687 23.73976625 14.6649641
#  15.17700342  3.81620663 29.18194848 20.68544417 22.32934783 28.01568563
#  28.58237108]
# 正规方程 - 均方误差为:
# 20.627513763095397
# 梯度下降 - 权重系数为:
# [-0.53087278  0.90066527 - 0.41998411  0.78452826 - 1.66411434  2.81985555
#  - 0.1400385 - 3.06040513  1.63836989 - 0.93857943 - 1.70111028  0.86004495
#  - 3.89817913]
# 梯度下降 - 偏置为:
# [22.63581926]
# 预测房价:
# [28.3384972  31.61218432 21.46396158 32.65581505 20.30729174 19.10061829
#  21.38069526 19.53714795 19.75519481 32.800326   21.36875982 27.27413464
#  15.63267453 19.98927317 36.99754756 18.67182959  9.69770926 18.70124007
#  30.83563162 24.33599091 19.06795404 34.05033349 29.50094527 17.39985907
#  34.80737074 26.48659296 34.31171118 27.41944575 19.08627983 15.87222231
#  30.79178744 14.51153831 37.45078101  8.67125435 16.46208808 16.83277864
#  7.68156071 19.80748244 40.48142444 29.2664118  25.31618817 17.8572737
#  39.25712808  6.68761008 21.56415312 25.05111149 20.88999669 20.69732958
#  17.02796236 26.26659763  9.66659845 27.17979966 30.62987402 16.65438921
#  9.58865169 35.4414963  31.47834199 22.986851   17.64076732 21.95875243
#  23.64418027 23.96574351 20.44045063 38.17989465 25.74351719 19.66462643
#  14.15722486  6.66995377 42.40651742 21.89014826 16.70608227 22.7040728
#  40.88428941 21.79554256 36.87164444 27.16304009 21.95214659 20.7841799
#  25.38449507 23.84834719 31.51118485 20.25375911 23.99097276 31.4576435
#  27.23684728 20.89030294 29.06532415 22.1043287  26.74748695 18.82579376
#  25.18329361 23.9334069  19.94497257 17.6087464  15.47370814 18.30864154
#  24.58487929 16.74665111 20.65366946 26.82001204 20.67787656 17.98854794
#  24.13807094 23.27245058 20.34099272 36.49425084 16.10123196 22.49570103
#  32.66186733 33.62779611 20.61225142 25.97666765 23.30780317 17.74838749
#  21.55604458 21.82380492 27.54772173 25.30744437 23.6853392  14.44559773
#  15.61858598  3.65291912 29.24019186 20.68377264 22.34013216 28.08768094
#  28.35643226]
# 梯度下降 - 均方误差为:
# 21.17625015763062

分析

回归当中的数据大小不一致，是否会导致结果影响较大。所以需要做标准化处理

• 数据分割与标准化处理
• 回归预测
• 线性回归的算法效果评估

回归性能评估

均方误差(Mean Squared Error) MSE评价机制
$$
M S E=\frac{1}{m} \sum_{i=1}^{m}\left(y^{i}-\bar{y}\right)^{2}
$$

tips：yⁱ为预测值，ȳ为真实值

• sklearn.metrics.mean_squared_error(y_true, y_pred)
  • 均方误差回归损失
  • y_true：真实值
  • y_pred：预测值
  • return：浮点数结果

对比

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大可以使用	需要计算方程，时间复杂度高O(n3)

选择：

• 小规模数据：
  • LinearRegression(不能解决拟合问题)
  • 岭回归
• 大规模数据：
  • SGDRegressor

扩展-关于优化方法GD、SGD、SAG

1、GD

梯度下降，原始的梯度下降法需要计算所有样本的值才能够得出梯度，计算量大，所以后面才会有一系列的改进

2、SGD

随机梯度下降，是一个优化方法，它在一次迭代时只考虑一个训练样本

• SGD的优点是：
  • 高效
  • 容易实现
• SGD的缺点是：
  • SGD需要许多超参数：比如正则项参数、迭代数
  • SGD对于特征标准化是敏感的

3、SAG

随机平均梯度法，由于收敛的速度太慢，有人提出SAG等基于梯度下降的算法

Scikit-learn：岭回归、逻辑回归等当中都会有SAG优化

---

4.2 欠拟合与过拟合

---

欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象(模型过于简单)

过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象(模型过于复杂)

原因以及解决办法

• 欠拟合原因以及解决办法
  • 原因：学习到数据的特征过少
  • 解决办法：增加数据的特征数量
• 过拟合原因以及解决办法
  • 原因：原始特征过多，存在一些嘈杂特征，模型过于复杂是因为模型尝试去兼顾各个测试数据点
  • 解决办法：正则化

4.2.1 正则化类别

1、L2正则化

• 作用：可以使得其中的一些W都很小，都接近于0，削弱某个特征的影响
• 优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象
• Ridge回归
• 加入L2正则化后的损失函数

$$
J(w)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{w}\left(x_{i}\right)-y_{i}\right)^{2}+\lambda \sum_{j=1}^{n} w_{j}^{2}
$$

tips：m为样本数，n为特征数

2、L1正则化

• 作用：可以使得其中的一些值直接为0，删除这个特征的影响
• LASSO回归

---

4.3 线性回归的改进-岭回归

---

---

4.4 分类算法-逻辑回归与二分类

---

---

4.5 模型保存和加载

---

---

4.6 无监督学习-K-means算法

---

---

4.7 总结

---